Задача
В Анчурии проходит чемпионат по шашкам в несколько туров. Дни и города проведения туров определяются жеребьёвкой. По правилам чемпионата никакие два тура не могут пройти в одном городе, и никакие два тура не могут пройти в один день. Среди болельщиков устраивается лотерея: главный приз получает тот, кто до начала чемпионата правильно угадает, в каких городах и в какие дни пройдут все туры. Если никто не угадает, то главный приз перейдёт в распоряжение оргкомитета чемпионата. Всего в Анчурии восемь городов, а на чемпионат отведено всего восемь дней. Сколько туров должно быть в чемпионате, чтобы оргкомитет с наибольшей вероятностью получил главный приз?
Решение
В таблице 8×8 нужно выбрать k ячеек так, чтобы в одном ряду и в одном столбце было выбрано не более одной ячейки. При этом число туров k нужно подобрать так, чтобы число Nk возможных вариантов выбора было наибольшим возможным.
(
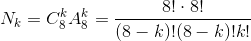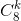– количество способов выбрать k городов из восьми без учета порядка, 
– количество способов выбрать k дней из восьми с учетом порядка, так как каждый из дней должен относиться к одному из городов).
Заметим, что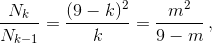 
где m = 9 – k. Поскольку m² < 9 – m только при m = 1, 2, то N1 < N2 < ... < N6 > N7 > N8.
Ответ
6 туров.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь