а) Пусть случайная величина X – число решённых задач по тригонометрии, Y – число решённых задач по геометрии и Z – число решённых задач по алгебре. Тогда сумма  U = X + Y + Z  есть общее число решённых задач. Мы хотим найти вероятность  P(U ≥ 5).  Проще вычислить

P(U < 5) = P(U = 0) + P(U = 1) + P(U = 2) + P(U = 3) + P(U = 4).

  Запишем таблицы распределения случайных величин X, Y и Z.

  Вероятность решить  0 ≤ k ≤ 3  задач по тригонометрии равна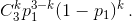  

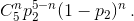
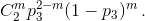
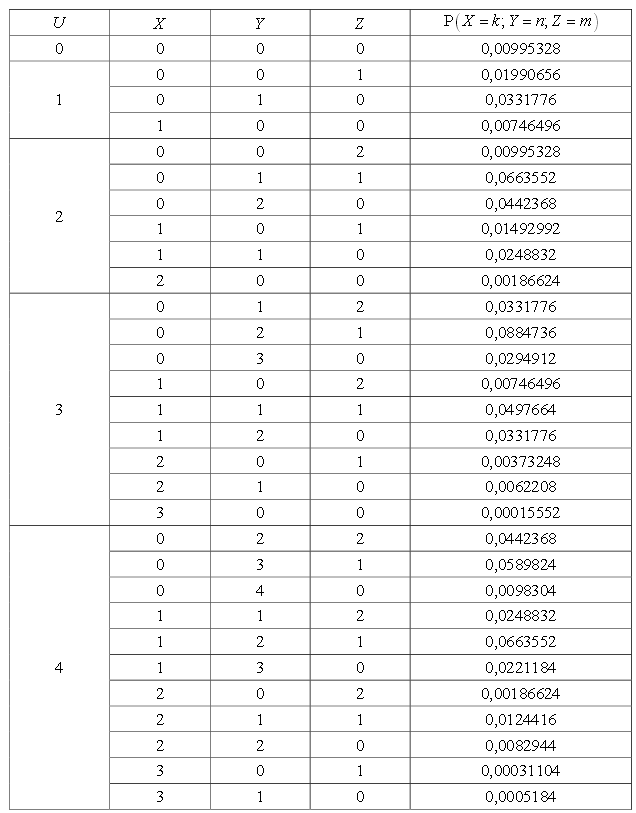
  Вероятность решить  0 ≤n≤ 5  задач по геометрии равна    И вероятность решить  0 ≤m≤ 2  задач по алгебре равна  Теперь заполним аналогичную таблицу дляU, представляя количество решённых задач в виде суммы различных слагаемых. При этом P(X = k,  Y = n,  Z = m) = P(X = k)P(Y = n)P(Z = m).  Вероятность  P(U = l)  получитьlбаллов есть сумма вероятностей каждого из случаев разбиенияl.  Искомая вероятность равна  P(U≥ 5) = 1 – P(U< 5) ≈ 0,27.   б) Способом, аналогичным указанному в пункте а), находим, что, если увеличить на 0,2 вероятность решения задач по тригонометрии, то вероятность решить не менее 5 задач  P(U ≥ 5)  станет равна  0,41752576 ≈ 0,42.

  Если увеличить на 0,2 вероятность решения задач по геометрии, получим  P(U ≥ 5) = 0,52636928 ≈ 0,53.

  Если же увеличить на 0,2 вероятность решения задач по алгебре, получим  P(U  5) = 0,35814546 ≈ 0,36.

  Таким образом, Ване следует заняться геометрией.   в) Вычислим математическое ожидание числа решённых задач  EU = EX + EY + EZ.  EX = EX₁ + EX₂ + EX₃,  где X_i равно 1 с вероятностью p₁, если i-я задача по тригонометрии решена, и 0 с вероятностью  1 – p₁,  если не решена. Значит,  EX_i = p₁,  откуда  EX = 3p₁.  Аналогично  EY = 5p₂,  EZ = 2p₃,  то есть  EU = 3p₁ + 5p₂ + 2p₃.

  Значит, при увеличении p₁ на 0,2 EU увеличится на 0,6, при увеличении p₂ на 0,2 – на 1, при увеличении p₃ на 0,2 – на 0,4.

  Таким образом, математическое ожидание числа решённых задач будет наибольшим в случае, если Ваня займётся геометрией.

а)  ≈ 0,27;   б)-в) геометрией.