Задача
По случаю начала зимних каникул все мальчики из 8 "В" пошли в тир. Известно, что в 8 "В" n мальчиков. В тире, куда пришли ребята, n мишеней. Каждый из мальчиков случайным образом выбирает себе мишень, при этом некоторые ребята могли выбрать одну и ту же мишень. После этого все одновременно делают залп по своим мишеням. Известно, что каждый из мальчиков попал в свою мишень. Мишень считается поражённой, если в нее попал хоть один мальчик.
а) Найти среднее количество поражённых мишеней.
б) Может ли среднее количество поражённых мишеней быть меньше n/2?
Решение
а) Обозначим через p вероятность того, что данная мишень поражена. В силу симметрии, искомое среднее число пораженных целей равно np.
Заметим, что вероятность того, что данный мальчик поразит данную мишень, равна 1/n. Следовательно, вероятность того, что данный мальчик не поразит данную мишень, равна 1 – 1/n. Поэтому (в силу независимости выстрелов) вероятность того, что ни один мальчик не поразит данную мишень равна (1 – 1/n)n. Значит, вероятность того, что хотя бы один мальчик поразит данную мишень, равна 1 – (1 – 1/n)n.
Таким образом, среднее количество поражённых мишеней равно n(1 – (1 – 1/n)n). б) Покажем, что среднее количество поражённых мишеней больше n/2. Для этого достаточно показать, что (1 – 1/n)n < ½.
Заметим, что последовательность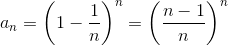 
возрастает. Действительно последовательность bn обратных чисел 
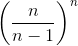убывает (см. решение задачи 161394 в).
Кроме того,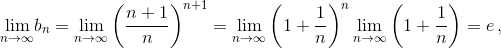 
следовательно, 
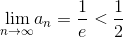(см. задачу 160873).
Ответ
а) n(1 – (1 – 1/n)n); б) не может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь