Задача
Неравнобедренный треугольник ABC вписан в окружность ω. Касательная к этой окружности в точке C пересекает прямую AB в точке D. Пусть I – центр вписанной окружности, треугольника ABC. Прямые AI и BI пересекают биссектрису угла CDB в точках Q и P соответственно. Пусть M – середина отрезка PQ. Докажите, что прямая MI проходит через середину дуги ACB окружности ω.
Решение
Можно считать, что точка D лежит на луче BA. Пусть L – середина дуги ACB.
∠CDB = ∠CAB – ∠ACD = ∠A – ∠B. Значит, ∠PQA = ∠QAB – ∠QDB = ½ ∠A – ½ (∠A - ∠B) = ½ ∠B. Первый способ. Пусть биссектрисы AI и BI углов треугольника пересекают ω вторично в точках A' и B' соответственно. ∠PQA = ½ ∠B = ∠B'A'A, поэтому PQ || A'B'.
Заметим, что ∠LA'A = ∠LBA = ½ (∠A + ∠B) = ∠B'IA. Значит, LA' || IB'. Аналогично, LB' || IA'. Поэтому IA'LB' – параллелограмм, и прямая LI делит A'B' пополам. Следовательно, она делит пополам и отрезок PQ, что и требовалось.
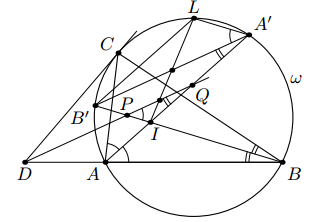
Пусть L' – точка окружности ω, диаметрально противоположная точке L. По лемме о трезубце (см. задачу 153119) L' – центр описанной окружности треугольника AIB. При этом ∠L'AL = ∠L'BL = 90°. Значит, LA и LB – касательные к описанной окружности треугольника AIB. Согласно задаче 156983 LI – симедиана треугольника AIB.
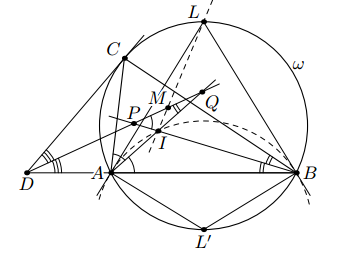
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь