Задача
Действительные числа a, b, c, d, по модулю большие единицы, удовлетворяют соотношению abc + abd + acd + bcd + a + b + c + d = 0.
Докажите, что 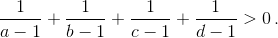
Решение
Обозначим 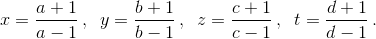 Поскольку модули чисел a, b, c, d больше единицы, числа x, y, z, t положительны (и не равны 1).
Поскольку модули чисел a, b, c, d больше единицы, числа x, y, z, t положительны (и не равны 1).
Данное соотношение переписывается в виде
(a + 1)(b + 1)(c + 1)(d + 1) = (a – 1)(b – 1)(c – 1)(d – 1),
или xyzt = 1. Из равенства 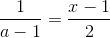 и аналогичных получаем, что
и аналогичных получаем, что 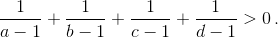 Таким образом, надо доказать, что x + y + z + t > 4.
Таким образом, надо доказать, что x + y + z + t > 4.
Поскольку xyzt = 1, но числа x, y, z, t отличны от единицы, среди них есть различные. Поэтому по неравенству Коши 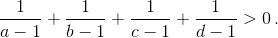
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет