Оценка. Первый способ.  y² = a²x² – a² + 1 < (ax)²,  значит,  y < ax.  Но y и ax – целые числа, поэтому  y ≤ ax – 1.  Следовательно,

a²x² – a² + 1 = y² ≤ (ax – 1)² = a²x² – 2ax + 1.  Стало быть,  2ax ≤ a², то есть  ^a/_x ≥ 2.

  Второй способ.  (ax – y)(ax + y) = a²x² – y² = a² – 1.  Числа  a² – 1  и  ax + y  положительны, поэтому число  k = ax – y  также положительно (и натурально). Следовательно, 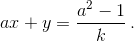    Отсюда  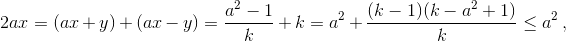  поскольку  1 ≤ k ≤ a² – 1.  Итак,  2ax ≤ a²,  то есть  ^a/_x ≥ 2.   Оценка достигается при  x > 100,  a = 2x,  y = ax – 1 = 2x² – 1.