Назад
Задача 165236 • Сложность: 3 • 9-11 класс
Задача

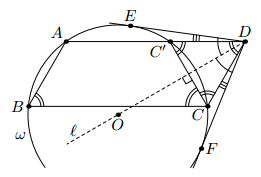
Параллелограмм ABCD таков, что  ∠B < 90°  и  AB < BC.  Точки E и F выбраны на описанной окружности ω треугольника ABC так, что касательные к ω в этих точках проходят через точку D. Оказалось, что  ∠EDA = ∠FDC.  Найдите угол ABC.

Авторы:
Якубов А.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Всероссийская олимпиада по математике 2014-2015 Заключительный этап
Количество версий:
4
Решение

  Пусть l – биссектриса угла EDF. Поскольку DE и DF – касательные, прямая l проходит через центр O окружности ω.

  Совершим симметрию относительноl. Так как  ∠EDA= ∠FDC,  лучDCперейдёт в лучDA. Посколькуlпроходит черезO, окружность ω перейдёт в себя; значит, точкаCпереходит в точкуC', лежащую наDAи на ω. При этом, так как  AD ≠ DC,  точкиC'иAразличны.   Из той же симметрии имеем  ∠DCC'= ∠DC'C.  Так как точкиA, B, CиC'лежат на ω, то  ∠DC'C= ∠ABC= ∠ADC.  Итак, все три угла треугольникаDCC'равны, откуда  ∠ABC= ∠CDC'= 60°.
Ответ

60°

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет