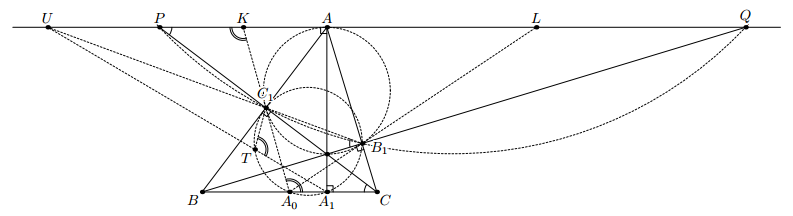
Пусть U – точка пересечения прямых PQ и B₁C₁ (см. рис.).

  Докажем сначала, что в одной точке пересекаются три окружности: описанные окружности Ω₁и Ω₂треугольниковPQA₁иA₁B₁C₁и окружность с диаметромAA₁.   Заметим, что четырёхугольникPQB₁C₁– вписанный. Действительно,  ∠APC₁= ∠BCC₁= ∠BB₁C₁.  Кроме того,UA– касательная к описанной окружности треугольникаAB₁C₁. Значит,  UA²=UC₁·UB₁=UP·UQ.  С другой стороны,UP·UQ– степень точкиUотносительно Ω₁, аUC₁·UB₁– степеньUотносительно Ω₂, то есть точкаUлежит на радикальной оси окружностей Ω₁и Ω₂. Поэтому вторая точкаTпересечения этих окружностей лежит наA₁U, и  UT·UA₁=UC₁·UB₁=UA².  Следовательно,UA– касательная к описанной окружности треугольникаTAA₁. Значит,AA₁– диаметр этой окружности.   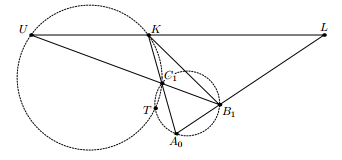Осталось доказать, чтоTпринадлежит также и описанной окружности треугольникаKLA₀, то есть чтоT–точка Микелядля прямыхUL, A₀L, KA₀,UB₁(см. рис.).  Для этого достаточно доказать, чтоTпринадлежит описанной окружности треугольникаUKC₁(см. задачу156628). Действительно, точкаTлежит на описанной окружности четырёхугольникаA₀C₁B₁A₁(окружности девяти точек треугольникаABC), поэтому  ∠C₁TA₁= ∠C₁A₀C= ∠UKC₁,  то есть четырёхугольникUKC₁T– вписанный.

Ответ задачи отсутствует