Задача
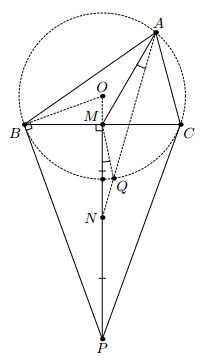
В треугольнике ABC M – середина стороны BC, P – точка пересечения касательных в точках B и C к описанной окружности, N – середина отрезка MP. Отрезок AN пересекает описанную окружность в точке Q. Докажите, что ∠PMQ = ∠MAQ.
Решение
Поскольку PB – касательная к окружности, а M – середина стороны BC, то треугольник BOP – прямоугольный с высотой BM, следовательно,
2NM·OM = PM·OM = BM².
Степень deg N точки N относительно описанной окружности треугольника ABC равна
NO² – OB² = (NM + OM)² – OB² = NM² + 2NM·OM + OM² – OB² = NM² + PM·OM + OM² – OB². С другой стороны, deg N = NQ·NA, то есть
NM² = NQ·NA.
Таким образом, MN – касательная к описанной окружности треугольника AMQ, откуда и следует равенство указанных углов.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь