Задача
Прямая l перпендикулярна одной из медиан треугольника. Серединные перпендикуляры к сторонам этого треугольника пересекают прямую l в трёх точках. Докажите, что одна из них является серединой отрезка, образованного двумя оставшимися.
Решение
Пусть прямая l перпендикулярна медиане BM, а серединные перпендикуляры к сторонам AB, AC, BC пересекают l в точках X, Y и Z (см. рис.). Точки K, M, L – середины этих сторон, O – центр описанной окружности, N – точка пересечения l и BM. Из перпендикулярности прямых следует, что
∠XOY = ∠BAC, ∠YOZ = ∠BCA, ∠OXZ = ∠ABM, ∠OZX = ∠CBM. Дальше можно рассуждать по-разному.
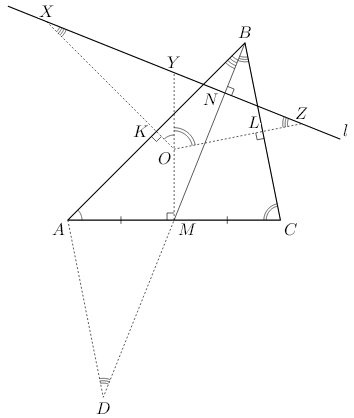
YZ : MB = YO : MC. Поскольку MA = MC, то YX = YZ. Второй способ. Продлим медиану BM на ее длину (см. риc.). Тогда треугольники BAD и XOZ подобны. Поскольку AM – медиана треугольника BAD и
∠BAM = ∠XOY, то OY – медиана треугольника XOZ, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь