Задача
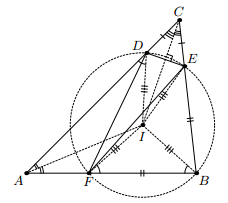
В треугольнике ABC на сторонах AC, BC и AB отметили точки D, E и F соответственно, так, что AD = AB, EC = DC, BF = BE. После этого стёрли всё, кроме точек E, F и D. Восстановите треугольник ABC.
Решение
Заметим, что серединные перпендикуляры к отрезкам DE и EF содержат биссектрисы треугольника ABC. Следовательно, центр описанной окружности треугольника DEF совпадает с центром I вписанной окружности треугольника ABC (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет