Задача
На гипотенузе AB прямоугольного треугольника ABC выбрана такая точка D, что BD = BC, а на катете BC – такая точка E, что DE = BE.
Докажите, что AD + CE = DE.
Решение
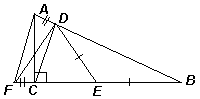
На продолжении катета ВС за точку С отложим отрезок CF = DA (см. рис.). Тогда ВА = BF, значит, ∠ ВАF = ∠ВFА. Следовательно, равны треугольники DАF и СFА (по двум сторонам и углу между ними), поэтому DF = CA. Тогда равны и треугольники BDF и АСВ (по трём сторонам). Значит, ∠BDF = ∠АСВ = 90°. Из равенства DE = BE следует, что DE – медиана прямоугольного треугольника BDF, проведённая к гипотенузе, то есть DE = BE = FЕ = FC + CE = AD + CE.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет