Задача
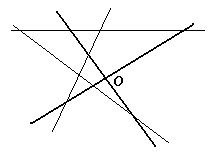
На листе бумаги были построены система координат (выделена жирно) и графики трёх функций: y = ax + b, y = bx + c и y = cx + a. После этого стёрли обозначения и направления осей, а сам лист как-то повернули (см. рисунок). Укажите на рисунке ось абсцисс и ее направление.
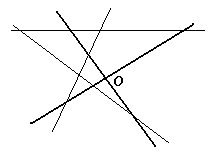
Решение
Первый способ. Так как графики попарно пересекаются, то среди чисел а, b, с нет одинаковых. Кроме того, коэффициенты в уравнениях переставлены "по циклу", значит, без ограничения общности можно считать, что a < b < c.
Найдём абсциссы точек попарного пересечения графиков и определим их знаки: 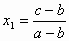 < 0,
< 0, 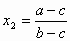 > 0,
> 0, 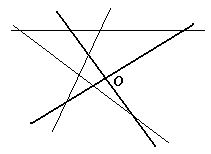 > 0. Выберем полуплоскость, ограниченную одной из осей, в которой располагаются ровно две точки пересечения графиков с положительными абсциссами. Из четырёх полуплоскостей она определяется однозначно. Эта полуплоскость ограничена осью ординат и именно в ней лежит положительная полуось абсцисс. Второй способ. Пронумеруем графики функций, например, так: (1) y = ax + b, (2) y = bx + c, (3) y = cx + a (см. рис.). Допустим, что направление на северо-запад является положительным направлением оси ординат. Тогда точки пересечения графиков с этой осью имеют координаты (0, b), (0, c) и (0, а) соответственно, причём a > b > 0 > c. Точки пересечения графиков с другой осью имеют координаты (– b/a, 0),
(– c/b, 0), (– a/c, 0), где
> 0. Выберем полуплоскость, ограниченную одной из осей, в которой располагаются ровно две точки пересечения графиков с положительными абсциссами. Из четырёх полуплоскостей она определяется однозначно. Эта полуплоскость ограничена осью ординат и именно в ней лежит положительная полуось абсцисс. Второй способ. Пронумеруем графики функций, например, так: (1) y = ax + b, (2) y = bx + c, (3) y = cx + a (см. рис.). Допустим, что направление на северо-запад является положительным направлением оси ординат. Тогда точки пересечения графиков с этой осью имеют координаты (0, b), (0, c) и (0, а) соответственно, причём a > b > 0 > c. Точки пересечения графиков с другой осью имеют координаты (– b/a, 0),
(– c/b, 0), (– a/c, 0), где
b/a < 0, – c/b > 0, – a/c > 0. Отсюда следует, что направление на юго-запад – это положительное направление оси абсцисс, но это противоречит тому, что положительное направление оси абсцисс должно совмещаться с положительным направлением оси ординат поворотом вокруг начала координат против часовой стрелки.
Если же предположить, что положительное направление оси ординат – на юго-восток, то a < b < 0 < c, поэтому знаки рассмотренных абсцисс не изменятся и противоречия не будет. Тем самым ось абсцисс будет направлена на юго-запад.
Два остальных случая возможного направления оси ординат (северо-восток и юго-запад) рассматриваются аналогично и приводят к противоречиям.
Ответ
См. рис. выше.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь