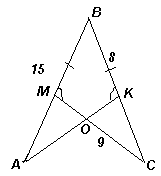
Задача
На сторонах угла ABC отмечены точки М и K так, что углы BMC и BKA равны, BM = BK, AB = 15, BK = 8, CM = 9.
Найдите периметр треугольника СOK, где O – точка пересечения прямых AK и СМ.
Решение
Треугольники ABK и CBM равны (по стороне и прилежащим углам, см. рис.). Поэтому ∠BCM = ∠BAK и CB = AB = 15, значит, CK = AM = 7.
Учитывая также, что ∠CKO = ∠AMO (они дополняют равные углы до развернутых), получим, что треугольники COK и AOM равны. Следовательно, OK = OM. Таким образом, PCOK = CK + CO + OK = CK + CO + OM = CK + CM = 16.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет