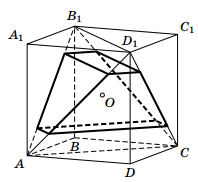
Первый способ. Отличный от куба шестигранник, в каждой вершине которого сходятся по три ребра (назовём его кубоидом), можно получить из правильного тетраэдра следующим образом. Рассмотрим куб ABCDA₁B₁C₁D₁ с центром O и правильный тетраэдр ACB₁D₁ (см. рис.).

  Две плоскости, параллельныеABCDи касающиеся вписанной сферы тетраэдраACB₁D₁, отсекают от этого тетраэдра две части. Оставшаяся часть тетраэдра представляет собой пример кубоида, удовлетворяющего условию задачи. Его вершины – это вершины двух прямоугольников (два сечения тетраэдра плоскостями), в силу симметрии все они равноудалены от центра кубаO, который также является центром вписанной сферы для тетраэдра (а значит, и для построенного кубоида).   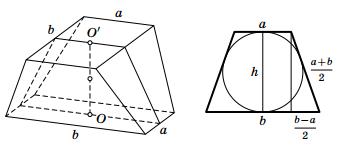Второй способ. Возьмём в некоторой плоскости прямоугольник с центром O и сторонами a и b  (b ≥ a),  повернём его относительно точки O на 90° и поднимем на высоту h над этой плоскостью (рис. слева). Получим новый прямоугольник с центром O'.   Восемь вершин двух прямоугольников (исходного и полученного) являются вершинами некоторого кубоида. Все эти вершины лежат на сфере с центром в середине отрезкаOO'. Выберемhтак, чтобы сфера с центром в середине отрезкаOO'и радиуса^h/₂касалась боковых граней кубоида. Для этого рассмотрим его сечение плоскостью, проходящей через прямуюOO'параллельно какой-нибудь паре сторон прямоугольника. Оно представляет собой равнобедренную трапецию с основаниямиaиb, в которую вписана окружность диаметраh(рис. справа). Боковые стороны этой трапеции равны^a+b/₂, поэтому  .

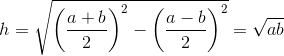
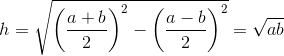Неверно.