Задача
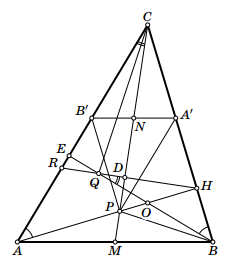
Дан треугольник ABC. Проведены высота AH и медиана CM. Обозначим точку их пересечения через P. Высота, проведённая из вершины B треугольника, пересекается с перпендикуляром, опущенным из точки H на прямую CM, в точке Q. Докажите, что прямые CQ и BP перпендикулярны.
Решение
Проведём через точку P прямые PA' и PB' так, чтобы точки A' и B' лежали на BC и AC соответственно и прямые PA' и PB' были параллельны AC и BC соответственно (см. рис.). Заметим, что ∠CAH = 90° – ∠ACH = ∠QBC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет