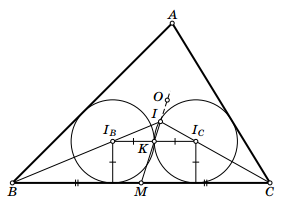
Обозначим центры двух равных окружностей, упомянутых в условии, соответственно I_B и I_C (см. рис.). Заметим, что  I_BI_C || BC,  так как расстояния от точек I_B и I_C до прямой BC равны. Следовательно, треугольники I_BII_C и BIC гомотетичны и их медианы IK и IM лежат на одной прямой. Но согласно условию это все та же прямая OI, то есть M, O, и I лежат на одной прямой. Значит, либо прямая OM – серединный перпендикуляр к стороне BC, либо точки M и O совпадают.

  В первом случаеIлежит на серединном перпендикуляре к сторонеBC, откуда следует равенство угловIBCиICB. Но тогда равны и углыBиC, а равнобедренность треугольникаABCзапрещена условием.   Во втором случае уголA– прямой, так как опирается на диаметрBCописанной окружности треугольникаABC.

90°.