Задача
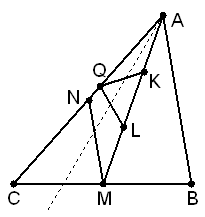
Точки K и L делят медиану AM треугольника ABC на три равные части, точка K лежит между L и . Отметили точку P так, что треугольники KPL и ABC подобны, причём P и C лежат в одной полуплоскости относительно прямой AM. Докажите, что P лежит на прямой AC.
Решение
Пусть N – середина AC. Первый способ. Рассмотрим на стороне AC такую точку Q, что ∠ALQ = ∠C. Тогда треугольники ALQ и ACM подобны (по двум углам). При этом подобии медиана MN треугольника ACM переходит в медиану QK треугольника ALQ. Следовательно, треугольник KQL подобен треугольнику NMC, а значит, и треугольнику ABC. Таким образом, точки P и Q совпадают.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет