Задача
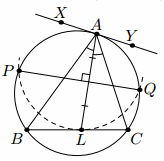
Пусть AL – биссектриса треугольника ABC. Серединный перпендикуляр к отрезкуAL пересекает описанную окружность Ω треугольника ABC, в точках P и Q. Докажите, что описанная окружность треугольника PLQ, касается стороны BC.
Решение
Заметим, что треугольники PLQ и PAQ симметричны относительно прямой PQ. Через точку A проведём касательную XY к окружности Ω. Достаточно доказать, что прямые XY и BC симметричны относительно прямой PQ. А поскольку точки A и L симметричны относительно прямой PQ, остаётся установить равенство углов XAL и BLA.
Используя касание и теорему о внешнем угле треугольника, имеем ∠XAL = ∠XAB + ∠BAL = ∠ACB + ∠CAL = ∠BLA.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет