Задачи и олимпиады по математике

Задача

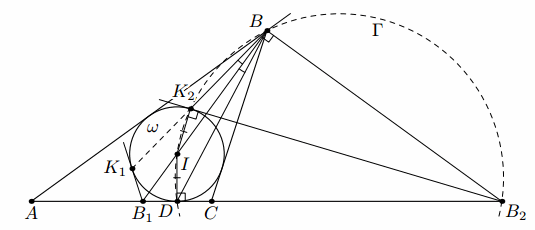
В неравнобедренном треугольнике ABC провели биссектрисы угла ABC и угла, смежного с ним. Они пересекли прямую AC в точках B₁ и B₂ соответственно. Из точек B₁ и B₂ провели касательные к окружности ω, вписанной в треугольник ABC, отличные от прямой AC. Они касаются ω в точках K₁ и K₂ соответственно. Докажите, что точки B, K₁ и K₂ лежат на одной прямой.

Решение

Обозначим через I центр окружности ω.

Пусть D – точка касания ω со стороной AC. Так как прямая BB₁ проходит через центр ω, точки D и K₁ симметричны относительно этой прямой, то есть BI – биссектриса угла K₁BD. Докажем, что BI также является биссектрисой угла K₂BD; отсюда будет следовать требуемое.

Рассмотрим окружность Г, построенную наB₂Iкак на диаметре. Так как BB₁⊥BB₂, аB₂K₂иB₂Dкасаются ω, то ∠B₂BI= ∠B₂K₂I= ∠B₂DI= 90°. Значит, точкиI, B, DиK₂лежат на Г. РадиусыIDиIK₂равны, поэтому равны и стягиваемые ими дуги окружности Г. Следовательно, ∠IBD= ∠IBK₂.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления