Задача
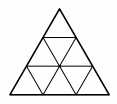
Правильный треугольник со стороной 3 разбит на девять треугольных клеток, как показано на рисунке. В этих клетках изначально записаны нули. За один ход можно выбрать два числа, находящиеся в соседних по стороне клетках, и либо прибавить к обоим по единице, либо вычесть из обоих по единице. Петя хочет сделать несколько ходов так, чтобы после этого в клетках оказались записаны в некотором порядке последовательные натуральные числа n, n + 1, ..., n + 8. При каких n он сможет это сделать?
Решение
Сумма исходных чисел равна 0, а за каждый ход сумма чисел изменяется на 2. Значит, она всегда чётна, то есть числа 1, 2, ..., 9 с суммой 45 получить нельзя.
Набор 2, 3, ..., 10 получить можно. Один из возможных способов представлен на рис. а)-в), где одинаковые числа показывают, к каким двум клеткам и сколько раз применяется операция прибавления единицы. Итоговый результат показан на рис. г).
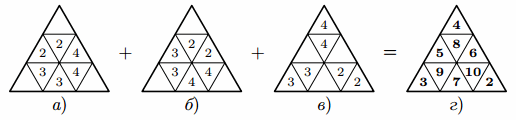
Ответ
Только при n = 2.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь