Задача
Биссектрисы углов A и C трапеции ABCD пересекаются в точке P, а биссектрисы углов B и D – в точке Q, отличной от P.
Докажите, что если отрезок PQ параллелен основанию AD, то трапеция равнобокая.
Решение
Обозначим через ρ(X, l) расстояние от точки X до прямой l. Поскольку точка P лежит на биссектрисе угла C, ρ(P, BC) = ρ(P, CD). Аналогично
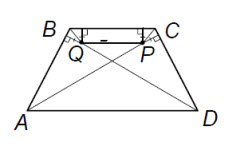
ρ(Q, B) = ρ(Q, BC). Поскольку QP || BC, ρ(Q, BC) = ρ(P, BC), откуда ρ(Q, AB) = ρ(P, CD) (см. рис.). Аналогично
ρ(P, AB) = ρ(P, AD) = ρ(Q, AD) = ρ(Q, CD).
Продолжим боковые стороны AB и CD до пересечения в точке S. Пусть точка P' симметрична Q относительно биссектрисы l угла ASD. Тогда из симметрии ρ(P', CD) = ρ(Q, AB) = ρ(P, CD) и ρ(P', AB) = ρ(Q, CD) = ρ(P, AB). Таким образом, точки P и P' лежат внутри угла ASD на прямых, параллельных AB и CD и отстоящих от них на расстояния ρ(P, AB) и ρ(P, CD) соответственно. Так как эти прямые не параллельны, у них только одна точка пересечения; значит, P' = P, точки P и Q симметричны относительно биссектрисы угла ASD, и l ⊥ PQ || AD.
Итак, в треугольнике SAD биссектриса является высотой, углы при его основании равны, то есть трапеция ABCD – равнобокая.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь