Задача
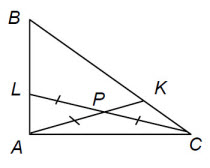
На гипотенузе BC прямоугольного треугольника ABC выбрана точка K так, что AB = AK. Отрезок AK пересекает биссектрису CL в её середине.
Найдите острые углы треугольника ABC.
Решение
Обозначим середину биссектрисы CL через P, а угол ABC через β; тогда ∠ACL = ½ (90° – β). В прямоугольном треугольнике ACL отрезок AP является медианой, поэтому AP = CP = LP. Теперь из равнобедренных треугольников APL и ABK получаем
∠ALP = ∠LAP = ∠BAK = 180° – 2∠ABK = 180° – 2β.
С другой стороны, ∠ALP = ∠ABC + ∠LCB как внешний угол в треугольнике BCL. Значит, 180° – 2β = β + ½ (90° – β), откуда 5β/2 = 135°, то есть
β = 54°. Тогда ∠ACB = 90° – ∠ABC = 36°.
Ответ
∠B = 54°, ∠C = 36°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет