Задача
В футбольном турнире участвовало 8 команд, причём каждая сыграла с каждой ровно по одному разу. Известно, что каждые две команды, сыгравшие между собой вничью, набрали в итоге разное число очков. Найдите наибольшее возможное общее число ничьих в этом турнире. (За выигрыш матча команде начисляется 3 очка, за ничью – 1, за поражение – 0.)
Решение
Оценка. Ясно, что максимум одна команда все свои 7 матчей сыграла вничью. Докажем, что ровно по 6 ничьих может быть не более, чем у двух команд. Действительно, любая такая команда набрала либо 6, либо 9 очков (в зависимости от того, выиграла или проиграла она свой результативный матч). Если таких команд три, то у двух из них поровну очков, значит, между собой они сыграли не вничью; этого не может быть, ибо они обе либо не выигрывали, либо не проигрывали ни одного матча. Таким образом, общее число ничьих не превосходит
(7 + 2·6 + 5·5) : 2 = 22.
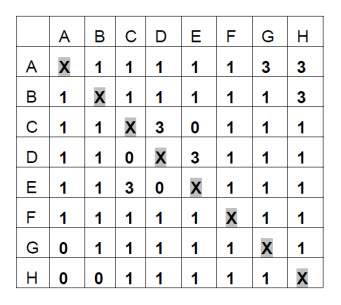
Пример на 22 ничьих показан в таблице:
Ответ
22 ничьих.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь