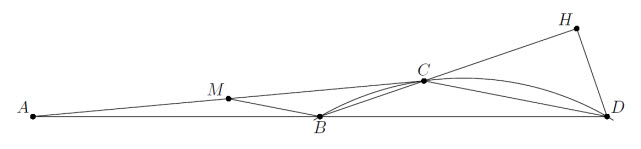
Зафиксируем вершины A, B, построим точку D, симметричную A относительно B, и возьмём точку C так, что  ∠BCD = 150°.  Тогда высота AK треугольника ABC равна высоте DH треугольника BCD, то есть  ½ CD.  С другой стороны, медиана BM является средней линией треугольника ACD, то есть тоже равна  ½ CD  (см. рис.). Будем теперь двигать точку C по дуге BD, вмещающей угол 150°. Когда C стремится к B, биссектриса CL угла ACB стремится к нулю, а медиана BM – к  ½ AB.  Когда C стремится к D, BM стремится к нулю, а  CL ≥ BC. Значит, существует положение точки C, при котором  CL = BM = AK.

Существует.