Задача
а) Существует ли треугольник, в котором наименьшая медиана длиннее наибольшей биссектрисы?б) Существует ли треугольник, в котором наименьшая биссектриса длиннее наибольшей высоты?
Решение
Пусть в треугольнике ABC длины сторон BC, AC, AB равны a, b, c соответственно, причём a ≤ b ≤ c, а AH – высота. а) Пусть CM – медиана, AL – биссектриса. Если угол C тупой или прямой, то AL > AC. Так как BC ≤ AC, то угол CMA – тупой или прямой, поэтому CM ≤ AC и, значит,
CM < AL. Пусть теперь угол C острый. Так как сторона AB наибольшая, то ∠C ≥ 60°. Тогда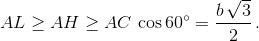  
В то же время
CM² = ¼ (2a² + 2b² – c²) ≤ ¼ (2a² + b²) ≤ ¾ b² ≤ AL². б) Пусть l – длина биссектрисы угла C, h = AH. Тогда (al + bl) sin C/2 = 2SABC = ab sin C, то есть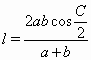 
. С другой стороны, h = b sin C и 
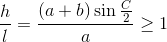(так как a + b ≥ 2a, а ∠C ≥ 60°).
Ответ
Не существует (в обоих случаях).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь