Назад
Задача 165038 • Сложность: 2 • 8-10 класс
Задача

Пусть AP и BQ – высоты данного остроугольного треугольника ABC. Постройте циркулем и линейкой на стороне AB точку M так, чтобы

∠AQM = ∠BPM.

Авторы:
Ясинский В.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VII Олимпиада по геометрии имени И.Ф. Шарыгина (2011 г.)
Количество версий:
4
Решение

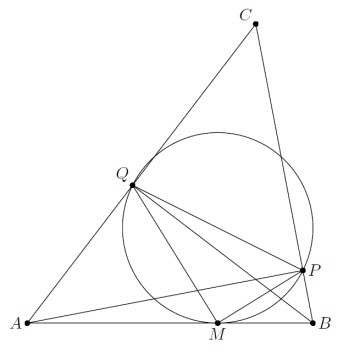
  Так как точки P, Q лежат на окружности с диаметром AB,  ∠BPQ = 180° – ∠A.  Значит,  ∠MPQ = ∠BPQ – ∠BPM = 180° – ∠A – ∠AQM = ∠AMQ.  Следовательно, окружность, проходящая через точки P, Q, M, касается прямой AB (см. рис.).

  Таким образом, наша задача сводится к задаче152450.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет