Задача
Вневписанная окружность прямоугольного треугольника ABC (∠B = 90°) касается стороны BC в точке A1, а прямой AC в точке A2. Прямая A1A2 пересекает (первый раз) вписанную окружность треугольника ABC в точке A'; аналогично определяется точка C'. Докажите, что AC || A'C'.
Решение
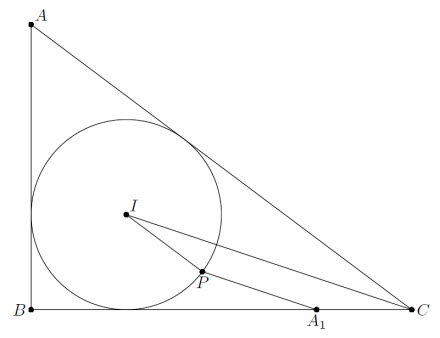
Пусть r – радиус вписанной окружности. Проведём через центр I вписанной окружности диаметр PQ, параллельный AC (см. рис.). Так как
∠PIC = ∠ACI = ∠BCI и CA1 = r = IP (см. задачу 155404), четырёхугольник IPA1C является равнобедренной трапецией. Значит, прямая A1P параллельна IC, то есть совпадает с A1A2. Соответственно, P совпадает с A', и аналогично Q совпадает с C'.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет