Задача
Окружность, вписанная в прямоугольный треугольник ABC (∠B = 90°), касается сторон AB, BC, CA в точках C1, A1, B1 соответственно. A2, C2 – точки, симметричные точке B1 относительно прямых BC, AB соответственно. Докажите, что прямые A1A2, C1C2 пересекаются на медиане треугольника ABC.
Решение
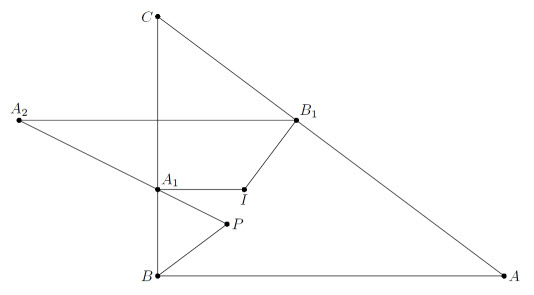
Пусть I – центр вписанной окружности, P – точка пересечения прямой A1A2 с медианой BB0 (см. рис.). Так как
∠IA1P = ∠IA1B1 = ½ ∠C = ½ ∠PBA1, то ∠BA1P = 90° – ∠PBA1, а ∠BPA1 = 180° – ∠PBA1 – (90° – ½ ∠PBA1) = 90° – ½ ∠PBA1 = ∠BPA1, то есть
BP = BA1. Так как BA1 = BC1, прямая C1C2 тоже проходит через P.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет