Задача
Вписанная окружность остроугольного треугольника ABC касается его сторон AB, BC, CA в точках C1, A1, B1 соответственно. Пусть A2, B2 – середины отрезков B1C1, A1C1 соответственно, O – центр описанной окружности треугольника ABC, P – одна из точек пересечения прямой CO с вписанной окружностью. Прямые PA2 и PB2 вторично пересекают вписанную окружность в точках A' и B'. Докажите, что прямые AA' и BB' пересекаются на высоте треугольника, опущенной на AB.
Решение
Достаточно доказать, что прямая AA' симметрична AP относительно биссектрисы угла A. Аналогично докажем, что BB' симметрична BP относительно биссектрисы угла B. Согласно задаче 156924 точка пересечения этих прямых лежит на прямой, симметричной CP относительно биссектрисы угла C, то есть на высоте треугольника (см. задачу 152358).
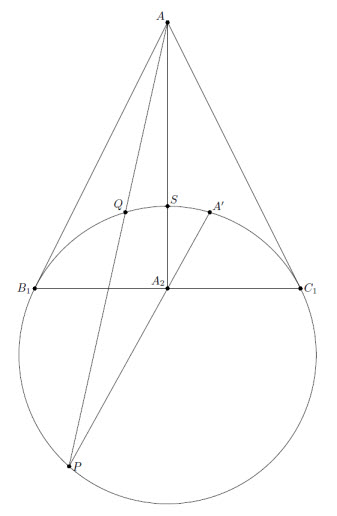
Пусть Q – точка пересечения прямой AP с вписанной окружностью ω, S – середина дуги B1C1 (см. рис.). Композиция проекций ω на себя из точек A и A2 меняет местами точки B1 и C1, переводит Q в A' и оставляет S на месте. Значит, равны двойные отношения (B1QSC1) = (C1A'SB1), то есть точки A' и Q симметричны относительно прямой AA2, что и требовалось.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь