Задача
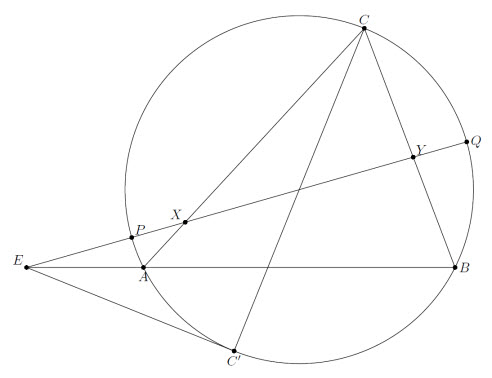
Четырёхугольник ABCD вписан в окружность с центром O. Точки C' и D' диаметрально противоположны точкам C и D соответственно. Касательные к окружности в точках C' и D' пересекают прямую AB в точках E и F (A лежит между E и B, B – между A и F). Прямая EO пересекает стороны AC и BC в точках X и Y, а прямая FO пересекает стороны AD и BD в точках U и V. Докажите, что XV = YU.
Решение
Достаточно доказать, что XO = OY. Действительно, тогда аналогично доказывается, что UO = OV, и, значит, XUYV – параллелограмм.
Пусть прямая EO пересекает окружность в точках P и Q (см. рис.). Искомое равенство равносильно равенству двойных отношений
(PXOY) = (QYOX). Спроецировав прямую EO на окружность из точки C, получим эквивалентное равенство (PAC'B) = (QBC'A), которое верно, так как прямые PQ, AB и касательная к окружности в точке C' пересекаются в одной точке.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь