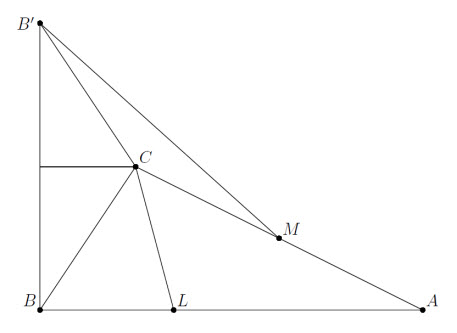
Решение 1:   Пусть  CL = l  – биссектриса,  CH = h  – высота,  BM = m  – медиана треугольника ABC, φ – острый угол, синус которого равен ^h/_l. Через p обозначим прямую, содержащую точку C и параллельную AB, а через B' – точку, симметричную точке B относительно прямой p.

  Выполнено хотя бы одно из равенств  ∠CLB = φ  или  ∠CLB = 180° – φ, . В первом случае

∠B'CM = 360° – 2∠CBA – ∠BCA = 2(180° – ∠CBA – ∠BCL) = 2φ  (см. рис.).

  Во втором случае аналогично проверяется, что угол B'CM также равен 2φ. Отсюда получаем следующее построение.

  Проведём две параллельные прямые на расстоянииhдруг от друга и отметим на одной из них точкуB; другая прямая будет прямойp. Далее отмечаем точкуB', а затем – точкуM, удалённую на расстояниеmотBи равноудалённую от параллельных прямых. Теперь строим две дуги окружностей с концами в точкахB'иMи угловой величиной  360° – 4φ.   ЕслиC₁иC₂– точки пересечения дуг с прямойp, аA_i (i= 1, 2)  – точка, симметричнаяC_iотносительноM, то каждый из треугольниковA₁BC₁иA₂BC₂является искомым.   Действительно, высоты этих треугольников, проведённые из вершинC₁,C₂, равныh, а отрезок  BM = m  является в каждом из них медианой. Кроме того, еслиL₁,L₂– основания соответствующих биссектрис, то из построения следует, что один из угловC₁L₁BиC₂L₂Bравен φ, а другой  180° – φ,  откуда  C₁L₁=C₂L₂=l.

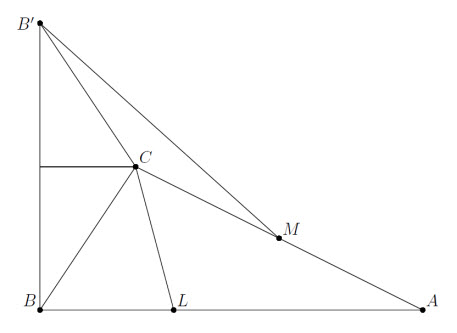
Решение 2:   Построим отрезок CL, равный данной биссектрисе, и проведём через L прямую AB, удалённую от C на расстояние h. Рассмотрим теперь следующее отображение этой прямой в себя. Для произвольной точки X найдём точку Y, удалённую от X и AB на расстояния, равные данной медиане BM и половине данной высоты CH (см. рис.). Затем отразим прямую CY относительно биссектрисы и найдём точку X' пересечения полученной прямой с AB. Очевидно, что это отображение сохраняет двойные отношения точек и переводит точку B в себя. Таким образом, задача сводится к известной задаче построения неподвижной точки проективного преобразования прямой (см. задачу 158459 б).

Ответ задачи отсутствует