Задача
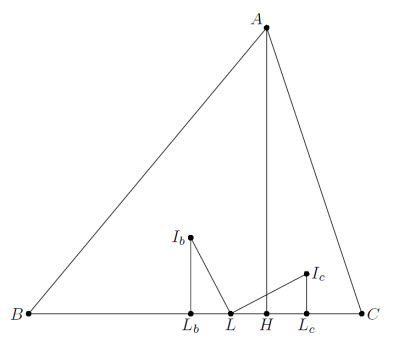
В треугольнике ABC проведена высота AH. Точки Ib и Ic – центры вписанных окружностей треугольников ABH и CAH; L – точка касания вписанной окружности треугольника ABC со стороной BC. Найдите угол LIbIc.
Решение
Пусть Lb, Lc – проекции точек Ib, Ic на BC, а rb, rc – радиусы вписанных окружностей треугольников AHB, AHC (см. рис.). Так как эти треугольники прямоугольные, то rb = ½ (AH + BH – AB), rc = ½ (AH + CH – AC), rb – rc = ½ (BH – CH) – ½(AB – AC) = (BH – CH) – ½(BL – CL) = LH. Следовательно, IbLb = rb = LLc, IcLc = rc = LLb, то есть треугольники LIbLb и IcLcL равны, LIb = LIc и ∠IbLIc = 90°. Таким образом, треугольник LIbIc – равнобедренный прямоугольный.
Ответ
45°
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет