Задача
Через вершину B треугольника ABC проведена прямая, перпендикулярная медиане BM. Эта прямая пересекает высоты, выходящие из вершин A и C (или их продолжения), в точках K и N. Точки O1 и O2 – центры описанных окружностей треугольников ABK и CBN соответственно. Докажите, что O1M = O2M.
Решение
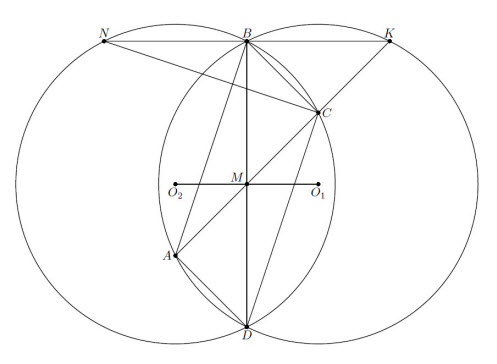
Достроим данный треугольник до параллелограмма ABCD (см. рис.). Заметим, что точки A и B лежат на окружности с диаметром KD. Следовательно, O1M ⊥ BD. Аналогично O2M ⊥ BD. Так как треугольники ABD и BCD равны, то равны и расстояния от центров их описанных окружностей до точки M.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет