Задача
На стороне BC равностороннего треугольника ABC взяты такие точки M и N (M лежит между B и N) , что ∠MAN = 30°. Описанные окружности треугольников AMC и ANB пересекаются в точке K. Докажите, что прямая AK содержит центр описанной окружности треугольника AMN.
Решение
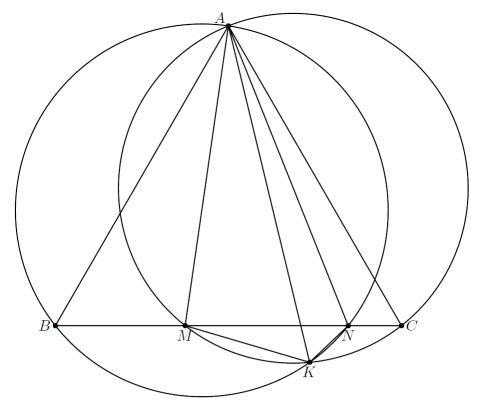
Так как ∠BAM + ∠NAC = ∠MAN и AB = AC, точка L, симметричная B относительно прямой AM, совпадает с точкой, симметричной C относительно прямой AN. Тогда ∠ALM = ∠ABM = ∠ACM, то есть L лежит на описанной окружности треугольника ACM. Аналогично L лежит на описанной окружности треугольника ABN и, значит, совпадает с K (см.рис.). Поэтому ∠KAN = ∠NAC = 30° – ∠BAM = 90° – ∠NMA. Но прямая, соединяющая A с центром описанной окружности треугольника AMN, образует с прямой AN такой же угол.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь