Задача
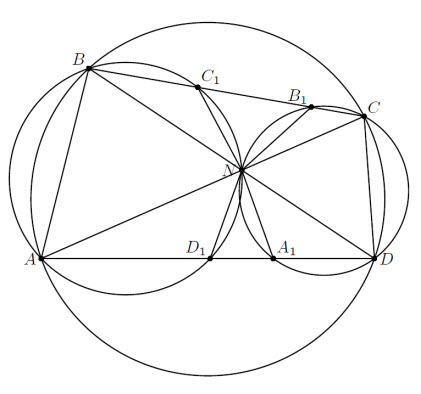
Диагонали вписанного четырёхугольника ABCD пересекаются в точке N. Описанные окружности треугольников ANB и CND повторно пересекают стороны BC и AD в точках A1, B1, C1, D1. Докажите, что четырёхугольник A1B1C1D1 вписан в окружность с центром N.
Решение
Рассматривая вписанный пятиугольник A1NB1CD, получаем, что A1N = B1N, так как равны опирающиеся на эти дуги углы BDA и BCA. Аналогично, NC1 = ND1. Кроме того, ∠NA1A = ∠ACD = ∠ABD = ∠DD1N (см. рис.). Следовательно, ND1 = NA1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет