Задача
В ряд записаны 20 различных натуральных чисел. Произведение каждых двух из них, стоящих подряд, является квадратом натурального числа. Первое число равно 42. Докажите, что хотя бы одно из чисел больше чем 16000.
Решение
Заметим, что 42 = 2·3·7, то есть все простые множители входят в его разложение в первой степени. Следовательно, чтобы произведение первых двух чисел являлось полным квадратом, второе число должно иметь вид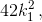 
где k1 – натуральное число.
Так как произведение второго и третьего числа – полный квадрат, то третье число, по тем же причинам, имеет вид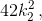 
где k2 – натуральное число, и так далее. Таким образом, все записанные числа, кроме первого, имеют вид 
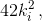где ki – натуральное число, отличное от единицы. Так как все числа различны, то наибольшее из чисел ki не может быть меньше чем 20. Следовательно, одно из записанных чисел не меньше чем
42·20² > 16000.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь