Назад
Задача 164997 • Сложность: 2 • 7-9 класс
Задача

В треугольнике ABC на сторонах AB, AC и BC выбраны точки D, E и F соответственно так, что  BF = 2CF,  CE = 2AE  и угол DEF – прямой.

Докажите, что DE – биссектриса угла ADF.

Разделы:
Планиметрия
Источники:
Московская математическая регата Олимпиады и турниры 2014/2015 8 класс
Количество версий:
3
Решение

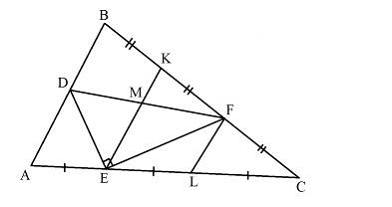
  Через точки Е и F проведём прямые, параллельные АВ. Пусть они пересекают ВС и АС в точках K и L соответственно (см. рис.). По теореме Фалеса K – середина отрезка BF, L – середина отрезка CE. Отметим точку M пересечения KE и DF, тогда M – середина отрезка DF.

  Таким образом,ЕМ– медиана прямоугольного треугольникаDEF, проведённая к гипотенузе, поэтому  ∠MDE= ∠MED.  Кроме того, из параллельности прямыхМЕиADследует, что  ∠MED= ∠EDA.  Значит,  ∠ADE= ∠FDE.
Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет