Задача
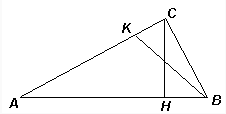
В прямоугольном треугольнике АВС проведена высота СН из вершины прямого угла. Из вершины В большего острого угла проведён отрезок BK так, что ∠CBK = ∠CАB (см. рис.). Докажите, что СН делит BK пополам.
Решение
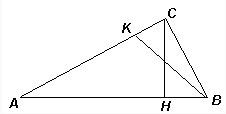
Пусть отрезки СН и BK пересекаются в точке D (см. рис.). Так как ∠BСН = ∠CАB = ∠CBK, то треугольник BDC – равнобедренный: CD = BD. Значит, CD – медиана прямоугольного треугольника BCK, то есть BD = KD.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет