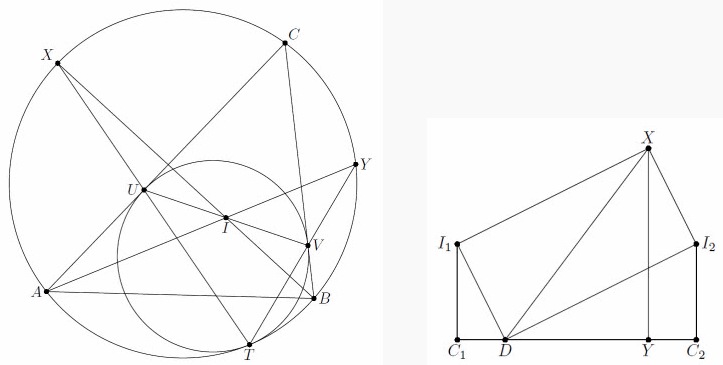
Лемма. Пусть окружность касается сторон AC, BC треугольника ABC в точках U, V, а описанной около него окружности изнутри в точке T. Тогда прямая UV проходит через центр I вписанной в треугольник ABC окружности.

  Доказательство. Пусть прямые TU, TV вторично пересекают описанную окружность в точках X, Y. Тогда X, Y – середины дуг AC, BC (см. задачу 152427), то есть прямые AY и BX пересекаются в точке I (рис. слева). Поэтому утверждение леммы следует из теоремы Паскаля, примененной к ломаной AYTXBC.

  Пусть I₁, I₂ – центры вписанных окружностей треугольников ACD, BCD. Из леммы следует, что отрезок XI₁ перпендикулярен биссектрисе угла ADC, а XI₂ – биссектрисе угла BDC, то есть DI₁XI₂ – прямоугольник (рис. справа). Пусть Y, C₁, C₂ – проекции точек X, I₁, I₂ на AB. Тогда  DC₁ = C₂Y,  DC₂ = C₁Y  и  BY – AY = BC₂ + C₂Y – AC₁ – C₁Y = (BC₂ – DC₂) – (AC₁ – DC₁) = (BC – CD) – (AC – CD) = BC – AC.  Следовательно, Y – точка касания стороны AB с вписанной окружностью.

Ответ задачи отсутствует