Задача
В треугольнике ABC середины сторон AC, BC, вершина C и точка пересечения медиан лежат на одной окружности.
Докажите, что она касается окружности, проходящей через вершины A, B и ортоцентр треугольника ABC.
Решение
Пусть C' – точка, симметричная C относительно середины AB. Тогда точки A, B, C' и ортоцентр треугольника ABC лежат на одной окружности (см. задачу 208949). С другой стороны, если A0, B0 – середины сторон BC, AC, то треугольник A0B0C гомотетичен треугольнику ABC' относительно центра тяжести M треугольника ABC с коэффициентом –½. Следовательно, описанные окружности этих треугольников касаются в точке M (см. рис.).
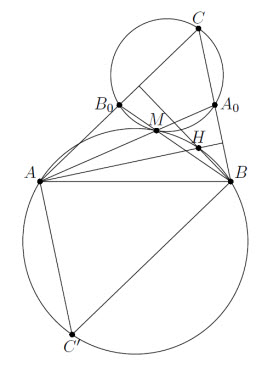
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет