Задача
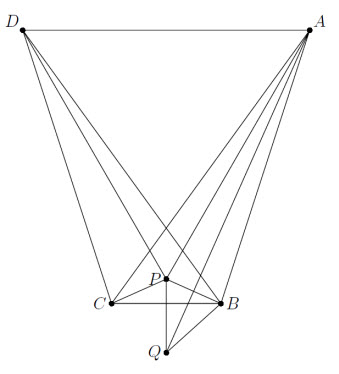
В треугольнике ABC ∠B = 2∠C. Точки P и Q на серединном перпендикуляре к стороне CB таковы, что ∠CAP = ∠PAQ = ∠QAB = ⅓ ∠A.
Докажите, что Q – центр описанной окружности треугольника CPB.
Решение
Пусть точка D симметрична A относительно PQ. Тогда ABCD – равнобокая трапеция, а диагональ BD – биссектриса угла B. Следовательно,
CD = DA = AB. Кроме того, ∠DAP = ∠C + ⅓ ∠A = ⅓ (∠A + ∠B + ∠C) = 60°. Поэтому треугольник ADP – равносторонний и AP = AB. Поскольку AQ – биссектриса угла PAB, то QP = QB = QC (см. рис.).
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет