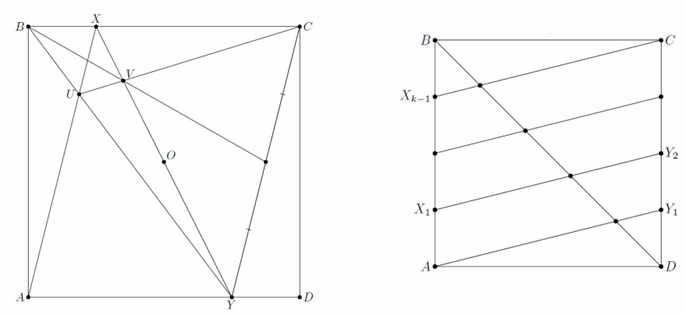
Сначала разделим сторону пополам. Проведя диагонали, найдём центр O квадрата ABCD. Теперь пусть X – точка на стороне BC, Y – точка пересечения XO и AD, U – точка пересечения AX и BY, V – точка пересечения прямых UC и XY (рис. слева). Тогда прямая BV делит основания трапеции CYUX пополам. Соединив O с серединой CY, разделим пополам стороны AB и CD.

  Покажем, что если две противоположные стороны разделены наkравных частей, то их можно разделить на  k+ 1  равных частей. Пусть AX₁=X₁X₂= ... =X_k–1B, DY₁=Y₁Y₂= ... =Y_k–1C.  Тогда по теореме Фалеса прямые  AY₁,X₁Y₂, ...,X_k–1C  делят диагональBDна  k+ 1  равных частей (рис. справа). Аналогично разделив вторую диагональ и проведя через соответствующие точки прямые, параллельныеBC, разделим на k+ 1  равных частей сторонуAB.

Ответ задачи отсутствует