Назад
Задача 164972 • Сложность: 3 • 8-10 класс
Задача

На плоскости отмечена точка M, не лежащая на осях координат. По оси ординат движется точка Q, а по оси абсцисс точка P так, что угол PMQ всегда остаётся прямым. Найдите геометрическое место точек N, симметричных M относительно PQ.

Авторы:
Акопян А. В.
Разделы:
Планиметрия
Источники:
Олимпиады и турниры Олимпиада по геометрии имени И.Ф. Шарыгина VII Олимпиада по геометрии имени И.Ф. Шарыгина (2011 г.)
Количество версий:
4
Решение

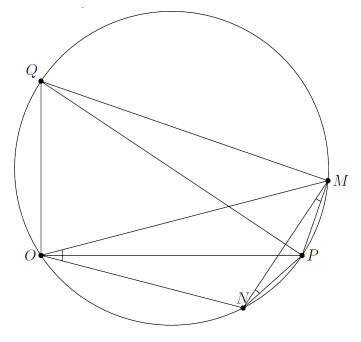
  Точки P, Q, M и начало координат O лежат на окружности с диаметром PQ. Значит, точка N тоже лежит на этой окружности и  ∠PON = ∠POM  (см. рис.). Таким образом, N лежит на прямой, симметричной OM относительно осей координат.

  С другой стороны, еслиN– произвольная точка этой прямой, аP, Q– точки пересечения осей координат с окружностьюOMN, то ∠PMN= ∠PON= ∠POM= ∠PNM  и  ∠PMQ= ∠POQ= ∠PNQ= 90°,  поэтому точкиMиNсимметричны относительноPQ.
Ответ

Прямая, симметричная OM относительно осей координат.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет