Задача
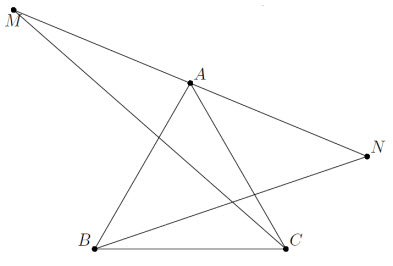
Через вершину A равностороннего треугольника ABC проведена прямая, не пересекающая отрезок BC. По разные стороны от точки A на этой прямой взяты точки M и N так, что AM = AN = AB (точка B внутри угла MAC). Докажите, что прямые AB, AC, BN, CM образуют вписанный четырёхугольник.
Решение
Так как треугольник BAN – равнобедренный, то ∠ANB = ½ ∠MAB (см. рис.). Аналогично ∠AMC = ½ ∠NAC. Значит, сумма этих углов равна 60°, а угол между прямыми BN и CM равен 120°, что равносильно утверждению задачи.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет