Задача
Петя вырезал из бумаги прямоугольник, положил на него такой же прямоугольник и склеил их по периметру. В верхнем прямоугольнике он провёл диагональ, опустил на неё перпендикуляры из двух оставшихся вершин, разрезал верхний прямоугольник по этим линиям и отогнул полученные треугольники во внешнюю сторону, так что вместе с нижним прямоугольником они образовали прямоугольник.
Как по полученному прямоугольнику восстановить исходный с помощью циркуля и линейки?
Решение
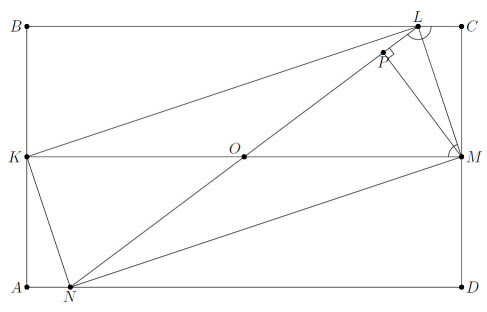
Пусть ABCD – полученный прямоугольник; O – его центр; K, M – середины его коротких сторон AB, CD; L, N – точки пересечения окружности с диаметром KM соответственно с BC и AD (см. рис.). Тогда прямоугольник KLMN – искомый. Действительно, пусть P – проекция M на LN. Так как
∠CLM = ∠OML = ∠MLO, то треугольники MCL и MPL равны и при перегибании по ML они совместятся. Аналогично при перегибании по MN совместятся треугольники MDN и MPN. Наконец, поскольку конструкция симметрична относительно точки O, то при перегибании по KL и KN треугольники BKL и AKN наложатся на треугольник NKL.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь