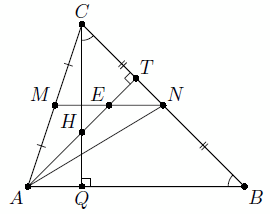
Пусть Н – ортоцентр треугольника АВС. Тогда высота АТ треугольника АВС содержит медиану треугольника AMN, то есть пересекает отрезок MN в его середине – точке Е. Далее можно рассуждать по-разному.   Первый способ. Треугольники ЕТN и АТВ подобны (рис. слева), следовательно,  TN : TB = TE : TA = EN : AB = 1 : 4.  Следовательно, СТ = ½ BT.

  Поскольку H – точка пересечения медиан треугольника AMN,  ЕН = ⅓ АЕ = ET.  Следовательно,  HТ = ½ AT.

  Значит, прямоугольные треугольники СТН и ВТА подобны, и  ∠ТСН = ∠ТВА.  Но СН – часть высоты CQ треугольника АВС, поэтому эти равные углы являются острыми углами прямоугольного треугольника CQВ.

 Второй способ. Отметим точкуK– середину стороныАВ(рис. справа).АМNK– параллелограмм, поэтому его диагональMKпроходит через серединуAN, а значит, и через точкуН.   Так как  МН || BC,  то треугольникиЕМНиЕNTравны (по стороне и двум прилежащим углам), значит,  ЕН = ЕТ.  МедианаCKтреугольникаАВСпроходит через точкуЕи делится в ней пополам, поэтомуCHKT– параллелограмм, то есть  TK || CH⊥AB.  Таким образом,TKявляется высотой и медианой прямоугольного треугольникаАТВ, значит, этот треугольник – равнобедренный.

45°.