Задача
В треугольнике ABC на стороне AB отметили точку D. Пусть ω1 и Ω1, ω2 и Ω2 – соответственно вписанные и вневписанные (касающиеся AB во внутренней точке) окружности треугольников ACD и BCD. Докажите, что общие внешние касательные к ω1 и ω2, Ω1 и Ω2 пересекаются на прямой AB.
Решение
Решение 1:Пусть I1, J1, I2, J2 – центры ω1, Ω1, ω2, Ω2, а K1, K2 – точки пересечения прямых I1J1, I2J2 с AB (см. рис.). Тогда I1K1 : I1C = J1K1 : J1C,
I2K2 : I2C = J2K2 : J2C и, дважды применив к треугольнику CK1K2 теорему Менелая, получим, что прямые I1I2 и J1J2 пересекают AB в одной и той же точке. Через эту точку проходят и общие внешние касательные.
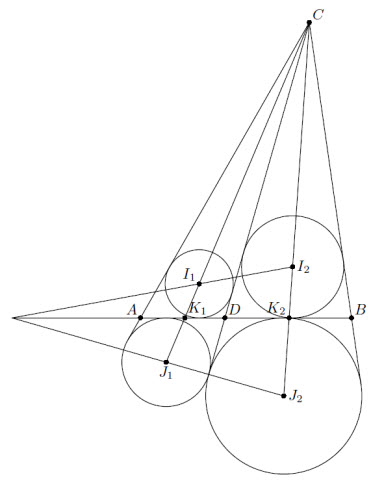
Решение 2:Пусть общие внешние касательные к окружностям ω1 и Ω2 пересекаются в точке P. Тогда, применив теорему о трёх колпаках (см. здесь) к тройкам окружностей ω1, Ω1, Ω2 и ω1, ω2, Ω2, получим, что точки пересечения общих внешних касательных сначала к окружностям Ω1, Ω2, а потом к ω1, ω2 являются точкой пересечения прямой PC с прямой AB, то есть совпадают и лежат на AB.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь