Задача
В тетраэдре АВСD: АВ = 8, ВС = 10, АС = 12, BD = 15. Известно, что четыре отрезка, соединяющие вершины тетраэдра с центрами окружностей, вписанных в противолежащие грани, пересекаются в одной точке. Найдите длины рёбер DA и DC.
Решение
Пусть отрезки DO1 и АО2, где O1 и О2 – центры вписанных окружностей треугольников ABC и DВС пересекаются в точке N (см. рис.). Тогда точки А, D, O1 и О2 лежат в одной плоскости, поэтому прямые АO1 и DО2 пересекают ребро ВС в одной и той же точке L. Так как AL и DL – биссектрисы треугольников ABC и DВС, то AB : AC = BL : CL = DB : DC. Следовательно, DC·AB = DВ·AC, откуда DC = 15·12 : 8 = 22,5.
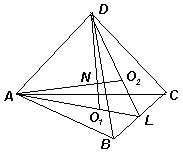
Ответ
DA = 18, DC = 22,5.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет