Задача
Четырёхугольник АВСD – вписанный. Лучи АВ и DС пересекаются в точке M, а лучи ВС и AD – в точке N. Известно, что ВМ = DN.
Докажите, что CM = CN.
Решение
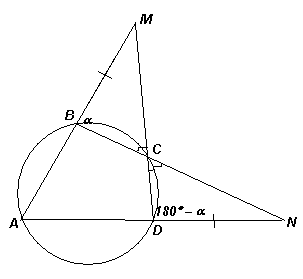
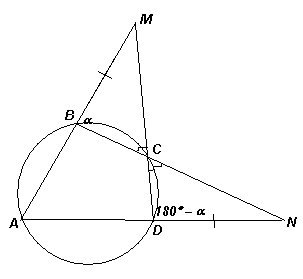
Пусть ∠MBC = α, тогда ∠CDN = ∠ABC = 180° – α (рис. слева). Далее можно рассуждать по-разному.
 и
и 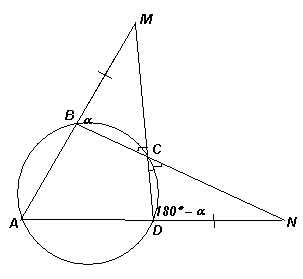 Так как
Так как
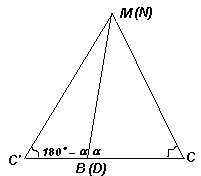
ВМ = DN, ∠ВСМ = ∠DCN, то CM = CN. Второй способ. "Отрежем" треугольник DСN и приложим его к треугольнику ВСМ, совместив равные отрезки DN и ВМ (рис. в центре). Так как
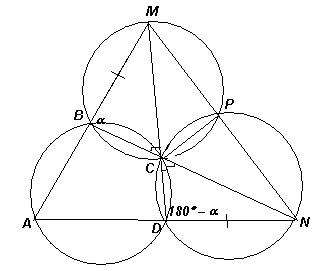
∠MBC + ∠CDN = 180°, то в результате образуется новый треугольник, в котором равны углы при вершинах С и C', значит, он – равнобедренный. Следовательно, CM = CN. Третий способ. Пусть описанная окружность треугольника ВСМ пересекает MN в точке Р (рис. справа). Тогда ∠NPC = ∠MBC = α, значит, точка Р лежит на описанной окружности треугольника DCN. Так как ВМ = DN и ∠ВСМ = ∠DCN, то радиусы этих окружностей равны. Углы CMN и CNM треугольника МСN опираются на равные дуги этих окружностей, поэтому эти углы равны. Следовательно, CM = CN.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь